|
Size: 1514
Comment:
|
Size: 4021
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| == Vorlesung Graphische Modelle == | == Vorlesung "Einführung in Graphische Modelle" == |
| Line 4: | Line 4: |
| || '''Termin:''' || || || '''Raum:''' || || || '''Dozent:''' || Dr. Ulf Brefeld, Dr. Marc Toussaint || || '''Ansprechpartner:''' || || |
||<(^|2> '''Vorlesung:''' || Dienstag 14.00-16.00 ||<^|6> {{attachment:bn.png|Bayesian Planning|width=190}} || || FR-6535 || ||<(^|2> '''Übung:''' || Dienstag 16.00-18.00 || || FR-4061 || ||<(^|2>'''Dozenten:''' || [[http://user.cs.tu-berlin.de/~brefeld|Dr. Ulf Brefeld]], [[http://user.cs.tu-berlin.de/~mtoussai|Dr. Marc Toussaint]] || || [[http://user.cs.tu-berlin.de/~lang|Tobias Lang]] (Übung)|| === Inhalt === Graphische Modelle definieren Warscheinlichkeitsfunktionen auf gekoppelten Variablen. Die gerichtete oder ungerichtete Graphstruktur erlaubt somit eine sehr flexible Modellierung von Variablen (=Knoten) und Anhängigkeiten zwischen Variablen (=Kanten). In den letzten Jahren wurden eine Reihe sehr mächtiger Inferenzalgorithmen (z.B. Viterbi Algorithmus, Junction Tree Algorithmus) entwickelt, die es uns erlauben graphische Modelle direkt für die Modellierung von natürlich auftretender Problemstellungen zu nutzen. Sie werden beispielsweise in der Handlungsplanung von Robotern und der maschinellen Sprach- und Bildverarbeitung erfolgreich eingesetzt. Desweiteren basieren viele aktuelle Verfahren des maschinellen Lernens wie z.B. Hidden Markov Models (HMM), Conditional Random Fields (CRFs) oder Structured Support Vector Machines (SSVM) auf graphischen Modellen. Die Vorlesung führt in die Grundlagen Graphischer Modelle ein und stellt sie anhand von praktischen Beispielen aus den genannten Gebieten (Robotik, Sprach- und Bildverarbeitung) vor. Thematisch beginnen wir mit einfachen Bayesschen Netzwerken, lernen dann verschiedene Inferenzmechanismen kennen und leiten schliesslich aktuelle Lernverfahren wie HMMs, CRFs und SSVMs her. Am Ende sollen die Teilnehmer in der Lage sein, beliebige Problemstellungen mit Hilfe von graphischen Modellen zu kodieren und zu lösen. === Voraussetzungen === gute Mathematikkenntnisse; Statistikkenntnisse sind nützlich, aber nicht zwingend erforderlich. === Übung === Es gibt jede Woche ein Übungsblatt. Voraussetzung zur Teilnahme an der Prüfung am Semesterende ist die erfolgreiche Bearbeitung der Hälfte aller Übungsaufgaben. Erfolgreiche Bearbeitung bedeutet, dass es ersichtlich wird, dass man sich mit der Aufgabe auseinandergesetzt und die zugrundeliegenden Themen prinzipiell verstanden hat. Blätter sind einzeln zu bearbeiten. Zu Beginn jeder Übung ist auf einer Liste anzukreuzen, welche Aufgaben man bearbeitet hat. Unter den möglichen Kandidaten wird einer per Zufall bestimmt, der die Aufgabe an der Tafel vorrechnet. Falls man an der Teilnahme der Übung verhindert ist, kann man ausnahmsweise seine Bearbeitung in der Vorlesung zuvor abgeben. |
| Line 11: | Line 52: |
| || '''Datum''' || '''Uhrzeit''' || '''Beschreibung''' || || 21.04. || 10:00-12:00 Uhr || Einführung mit Überblick || || 28.04. || 10:00-12:00 Uhr || Diskrete Wahrscheinlichkeitsverteilungen, Graphische Modelle, Faktorgraphen, Bedingte und Gesamtwahrscheinlichkeiten || || 5.05. || 10:00-12:00 Uhr || Inferenz, Eliminierungsalgorithmus, Evidenzen || || 12.05. || 10:00-12:00 Uhr || Summen-Produkt-Algorithmus, Junction Tree Alg. || || 19.05. || 10:00-12:00 Uhr || Beliefpropagierung in zyklischen Graphen, Mean-Field Alg. || || 26.05. || 10:00-12:00 Uhr || Hidden Markov Models, Forward-Backward Alg., Viterbi, Expectation-Maximization (EM) || || 2.06. || 10:00-12:00 Uhr || Bedingte Wahrscheinlichkeiten, (Kernel-) Conditional Random Fields (CRFs), Features, Optimierung || || 9.06. || 10:00-12:00 Uhr || Optimierung (Fortsetzung), Strukturiertes Perzeptron || || 16.06. || 10:00-12:00 Uhr || Strukturierte Support-Vector Maschinen || || 16.06. || 10:00-12:00 Uhr || Influence Diagramme || || 16.06. || 10:00-12:00 Uhr || Markov Decision Processes || || 16.06. || 10:00-12:00 Uhr || Inferenz für Planen, Optimale Handlungsanweisungen (Policies) || ---- || 16.06. || 10:00-12:00 Uhr || Zusammenfassungen und Fragestunde || |
|| '''Datum''' || '''Beschreibung''' || Vorlesung || Übung || || 21.04. || Einführung mit Überblick || [[attachment:01.pdf|vl01]] [[attachment:01_4up.pdf|vl01_4up]] || [[attachment:ex1.pdf|ex1]] || || || || || 28.04. || Diskrete Wahrscheinlichkeitsverteilungen, Bedingte und Gesamtwahrscheinlichkeiten, Graphische Modelle, Faktorgraphen || || 05.05. || Inferenz, Eliminierungsalgorithmus, Evidenzen || || 12.05. || Summen-Produkt-Algorithmus, Junction Tree Alg. (JTA) || || 19.05. || Beliefpropagierung in zyklischen Graphen (Loopy BP), Mean-Field Alg. || || || || || 26.05. || Hidden Markov Models (HMMs), Forward-Backward Alg., Viterbi, Expectation-Maximization (EM) || || 02.06. || Bedingte Wahrscheinlichkeiten, (Kernel-) Conditional Random Fields (k-CRFs), Features, Optimierung || || 09.06. || Optimierung (Fortsetzung), Strukturiertes Perzeptron || || 16.06. || Strukturierte Support-Vektor-Maschinen (SSVMs) || || || || || 23.06. || Influence Diagramme || || 30.06. || Markov Decision Processes (MDPs) || || 07.07. || Inferenz für Planen, Optimale Handlungsanweisungen (Policies) || || || || || 14.07. || Zusammenfassung und Fragestunde || |
Describe Main/SS09_GraphicalModels here.
Vorlesung "Einführung in Graphische Modelle"
Vorlesung:
Dienstag 14.00-16.00
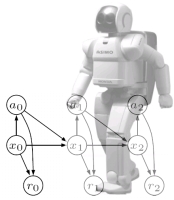
FR-6535
Übung:
Dienstag 16.00-18.00
FR-4061
Dozenten:
Tobias Lang (Übung)
Inhalt
Graphische Modelle definieren Warscheinlichkeitsfunktionen auf gekoppelten Variablen. Die gerichtete oder ungerichtete Graphstruktur erlaubt somit eine sehr flexible Modellierung von Variablen (=Knoten) und Anhängigkeiten zwischen Variablen (=Kanten).
In den letzten Jahren wurden eine Reihe sehr mächtiger Inferenzalgorithmen (z.B. Viterbi Algorithmus, Junction Tree Algorithmus) entwickelt, die es uns erlauben graphische Modelle direkt für die Modellierung von natürlich auftretender Problemstellungen zu nutzen. Sie werden beispielsweise in der Handlungsplanung von Robotern und der maschinellen Sprach- und Bildverarbeitung erfolgreich eingesetzt. Desweiteren basieren viele aktuelle Verfahren des maschinellen Lernens wie z.B. Hidden Markov Models (HMM), Conditional Random Fields (CRFs) oder Structured Support Vector Machines (SSVM) auf graphischen Modellen.
Die Vorlesung führt in die Grundlagen Graphischer Modelle ein und stellt sie anhand von praktischen Beispielen aus den genannten Gebieten (Robotik, Sprach- und Bildverarbeitung) vor. Thematisch beginnen wir mit einfachen Bayesschen Netzwerken, lernen dann verschiedene Inferenzmechanismen kennen und leiten schliesslich aktuelle Lernverfahren wie HMMs, CRFs und SSVMs her. Am Ende sollen die Teilnehmer in der Lage sein, beliebige Problemstellungen mit Hilfe von graphischen Modellen zu kodieren und zu lösen.
Voraussetzungen
gute Mathematikkenntnisse; Statistikkenntnisse sind nützlich, aber nicht zwingend erforderlich.
Übung
Es gibt jede Woche ein Übungsblatt. Voraussetzung zur Teilnahme an der Prüfung am Semesterende ist die erfolgreiche Bearbeitung der Hälfte aller Übungsaufgaben. Erfolgreiche Bearbeitung bedeutet, dass es ersichtlich wird, dass man sich mit der Aufgabe auseinandergesetzt und die zugrundeliegenden Themen prinzipiell verstanden hat. Blätter sind einzeln zu bearbeiten. Zu Beginn jeder Übung ist auf einer Liste anzukreuzen, welche Aufgaben man bearbeitet hat. Unter den möglichen Kandidaten wird einer per Zufall bestimmt, der die Aufgabe an der Tafel vorrechnet. Falls man an der Teilnahme der Übung verhindert ist, kann man ausnahmsweise seine Bearbeitung in der Vorlesung zuvor abgeben.
Termine
Datum
Beschreibung
Vorlesung
Übung
21.04.
Einführung mit Überblick
28.04.
Diskrete Wahrscheinlichkeitsverteilungen, Bedingte und Gesamtwahrscheinlichkeiten, Graphische Modelle, Faktorgraphen
05.05.
Inferenz, Eliminierungsalgorithmus, Evidenzen
12.05.
Summen-Produkt-Algorithmus, Junction Tree Alg. (JTA)
19.05.
Beliefpropagierung in zyklischen Graphen (Loopy BP), Mean-Field Alg.
26.05.
Hidden Markov Models (HMMs), Forward-Backward Alg., Viterbi, Expectation-Maximization (EM)
02.06.
Bedingte Wahrscheinlichkeiten, (Kernel-) Conditional Random Fields (k-CRFs), Features, Optimierung
09.06.
Optimierung (Fortsetzung), Strukturiertes Perzeptron
16.06.
Strukturierte Support-Vektor-Maschinen (SSVMs)
23.06.
Influence Diagramme
30.06.
Markov Decision Processes (MDPs)
07.07.
Inferenz für Planen, Optimale Handlungsanweisungen (Policies)
14.07.
Zusammenfassung und Fragestunde